ad2math.com

العدد الذهبي يساوي تقريباً 1.618033988 وقد سمي بالعدد الذهبي نسبة للمستطيل الذهبي، المستطيل الذي طوله x وعرضه واحد ، لو اقتطعنا منه مربع طول ضلعه واحد لبقي مستطيل يتناسب بعداه مع بعدي المستطيل الأصلي، و العدد الذهبي هو الحل الموجب للمعادلة:x²-x-1. وجده fidais وهو العدد الذي استعمله قدماء المصريين في بناء الأهرامات والرومان في بناء المسارح وهو كذالك أساس لمتتالية فيبوناتشي التي حدودها 5,8,13,21,34....التي أوجدها من تأمله لزهرة.

المستطيل التالي طوله x وعرضه واحد ، لو اقتطعنا منه مربع طول ضلعه واحد لبقي مستطيل يتناسب بعداه مع بعدي المستطيل الأصلي. . هذا المستطيل أطلق عليه المستطيل الذهبي ، وهناك رسوم هندسية مشابهة لهذا المستطيل وجدت في بعض المواقع الأثرية. ومن الشكل السابق يمكن التعبير عن التناسب بالشكل التالي :

حلها هو

قوى العدد الذهبي

الحلزون الذهبية: انطلاقا من مستطيل ذهبي كبير و بعد قطع المربع كما في الشكل أعلاه، نقوم بإنشاء أرباع أقواس دوائر شعاعها طول ضلع المربع المقطوع.

جانبا هناك حلزونات في الطبيعة يعطيها العدد جمالية، سبحان الخالق.

خماسي الأضلاع المنتظم، هو خماسي أضلاع، أضلاعه كلها متقايسة، و زواياه أيضا كلها متقايسة، يكون دائما محاط بدائرة مركزها هو مركز المضلع، قياس زوايا الخماسي الأضلاع المنتظم هو:

AC/AB ------- 108° =

المثلثان ABC و ACD هما مثلثان متساويا الساقين في Aو Dعلى التوالي و هما أيضا مثلثان ذهبيان ، ذلك راجع للعلاقة التناسبية بين اضلاعهما و التي معاملها العدد الذهبي

كذلك تكاثر النحل فهو أيضا يخضع لمتتالية فيبوناتشي:

العدد الذهبي في الطبيعة:
التناسب بشكل عام (حتى لو لم يكن تبعاً للنسبة الذهبية) هو واحد من أكبر أسرار الجمال، فالوجه الحسن يكون جميلاً بوجود تناسب مُتزن بين أطوال أجزائه، والسيارة تكون جميلة إذا ما جاءت أطوالها متناسبة بشكل يريح الناظر، وحتى قطع الأثاث والأدوات الصغيرة وكل ما يحيط بنا سوف يغدو جميلاً في حال كانت أطواله متناسبة رياضياً ولم تكن عشوائية الأطوال. بل حتى التوقيت الزمني للأشياء يكون جميلاً إذا توالى في تناسب مدروس.

إن النسبة الذهبية موجودة حولنا في الطبيعة، بل موجودة في تركيبة أجسادنا، كما تتواجد النسبة الذهبية حولنا في الحيوانات وبعض أنواع الأشجار بأكثر من صورة، بين الجذع فالأغصان فالفروع حتى الأوراق.

لقد أكتشف المهتمون بالأمر أن جسم الإنسان مُقسم حسب النسبة الذهبية وذلك عدة مرات. إن السُرّة تقسم جسم الإنسان إلى قسمين غير متساويين، النسبة بينهما هي أقرب ما يكون إلى النسبة الذهبية.وأكثر من ذلك أن القسم العلوي من جسم الإنسان (من السُرّة إلى قمة الرأس) يُقسِم أيضاً إلى قسمين غير متساويين، النسبة بينهما كالنسبة الذهبية وذلك عند الحنجرة (أنظر الشكل)، أمّا القسم السُفلي (من السُرّة إلى أخر القدمين) فهو مقسوم أيضاً (بواسطة الركبة هذه المرّة) إلى قسمين بالنسبة الذهبية.

كما توجد النسبة الذهبية بين نصف الكف إلى نصف الإصبع، وغيره من أقسام الإصبع.
إن جئنا للعمارة فيُمكن مُلاحظة حضور النسبة الذهبية في كثير مما يحيط بنا سواء بُقصد من المعماري، أو بدافع لا واعي منه. أما تاريخياً فتأتي الأهرامات في مقدمة المعالم التي خضعت للنسبة الذهبية بالرغم مِن أنها لم تكن قد أُكتشفت علمياً بعد، بينما يُعتبر "الباراثينون" أحد أشهر معالم اليونان التي تقوم على النسبة الذهبية عن قصد، ورغم كل الأضرار التي لحقت به مع توالي القرون المديدة، فقد ظل محافظاً على جوهر جماله. ويأتي جامع عقبة في القيروان ليكون العمل الأشهر من العمارة الإسلامية الذي مثل النسبة الذهبية في كثير من أجزاءه، من المساحة الكلية، إلى مساحة فناء المسجد، إلى حتى التناسب المبهر في المنارات.

جيب تمام زاوية من ذهب

ويعني أن:

في الصورتين العلويتين صورتين للمسرح الروماني الكوليزيم.

في الصورة جانبا البانتاكون الأمريكي ، والذي سمي انطلاقا من شكله الذي هو على شكل خماسي أضلاع منتظم.

ليوناردو فيبوناتشي (بيزا، 1170 - 1250) عالم رياضيات إيطالي. وقد اشتهر حديثا باسم فيبوناتشي، وكان يعرف فيما مضى باسم ليوناردو بيزانو (نسبة إلى مدينته بيزا)، كما كان يعرف باسم ليوناردو بيقوللو (وتعني Bigollo المسافر)، لكن اسمه الحقيقي كان ليوناردة قيلييلمي (Leonardo Gulielmi).
ولد فيبوناتشي في مدينة بيزا بإيطاليا. وقد كان تعليمه بالأساس في شمال إفريقيا ذلك أن والده قيلييلمو بوناتشي كان مشرفا على أسواق بيزا في الجزائر وتونس والمغرب... وقد جلب فيبوناتشي من هذه الأماكن، حسبما قيل، سنة 1200، الأرقام العربية المستعملة اليوم والتعاليم الجبرية وقد قيل أيضا أن من فعل ذلك كان جيربير دوريلاك. وفي سنة 1202، أصدر كتابا بعنوان "ليبر أباشي"، المهتم بالحسابات والمحاسبة. وقد تأثر فيبوناتشي في هذا الكتاب بحياته في الدول العربية، ومما يدلّ على ذلك أن فبيوناتشي قد قام بتحرير جزء منه من اليمين إلى اليسار. وبنشر هذا الكتاب قام فيبوناتشي بتعريف الأوروبيين على أنظمة الحساب والكتابة العربية. وقد كان هذا النظام يفوق بمراحل النظام الروماني المعتمد آنذاك في أوروبا، وكان فيبوناتشي على دراية بذلك. لكن هذا النظام واجه عنتا كبيرا قبل أن ينتشر بصورة عظيمة.
و قد اشتهر فيبوناتشي أساسا بسيبب مسألة تقودنا إلى متتالية فيبوناتشي، ولكنه عرف فيما مضى بسبب تطبيقه للأريثماطيقية على الحساب التجاري : حساب المرابيح، تحويل العملات.. لكن أعماله المتعلقة بنظريّة الأعداد أهملت في حياته. وفي دراسة صغيرة أجريت حوله لاحقاـ تم اكتشاف طرائق خفية كان يستعملها نجدها حتى في بعض جوانب البورصة (التحليل التقني). واسم فيبوناتشي الذي يعني ابن بوناتشي أطلق عليه به بعد وفاته.

متتالية فيبوناتشي هي متتالية أعداد صحيحة طبيعية موجبة مُعرَفة بعلاقة التراجع التالية: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 …

هناك علاقة ما بين نشأة القانون التراجعي ومتوالية فيبوناتشي. تلك المتوالية التي نشأت بأعقاب مسألة زوج الأرانب المشهورة وهي:

عندنا زوج أرانب (وُلدت حديثاً)، هذا الزوج ينجب عندما يبلغ الشهرين. وكل زوج يستطيع الإنجاب زوج أرانب إضافي كل شهر. ما هو عدد الأزواج بعد 10 أشهر؟

هيا بنا نتعقب عدد أزواج الأرانب شهراًً بعد شهر:

1.     بالبداية كان هناك زوج أرانب فقط زوج واحد.

2.     بعد شهر بقي زوج الأرانب كما هو لأن الأرانب لا تتكاثر إلا عندما تبلغ الشهرين زوج واحد.

3.     في نهاية الشهرين وُلِد زوج أرانب زوجان.

4.     في نهاية الثلاث أشهر زوج واحد يستطيع الإنجاب ولذلك وُلد زوج آخر 3 أزواج.

5.     في نهاية الأربعة أشهر زوجان يستطيعان الإنجاب لذلك وُلد زوجان آخران من الأرانب 5 أزواج.

6.     في نهاية الخمسة أشهر3 أزواج تستطيع الإنجاب ولذلك وُلد 3 أزواج إضافية 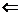8 أزواج.

الآن يمكن الملاحظة أنه في نهاية كل شهر يُضاف إلى الأزواج التي كانت في نهاية الشهر السابق أزواج بنفس عدد الأزواج التي كانت قبل شهرين، ومن هنا تأتي متتالية فيبوناتشي.

يمكن شرح تكاثر الأرانب خلال الرسم:

1

2

3

4

5

6

المثلث الذهبي:

هناك طريقة أخرى للحصول على نسبة ذهبية، وذلك يتم من خلال بناء مثلث متساوي الساقين بحيث أن زاوية الرأس تساوي 36ْ، وزوايا قاعدته يساويان 72ْ. كما في الشكل أدناه:

إذا كانت طول القاعدة المثلث المتساوي الساقين 1، وكان طول ساقيه φ. لكي نثبت ذلك، نُنصف إحدى زوايا القاعدة. فنحصل على مثلث صغيرزواياه مساوية لـ36ْ،72ْ،72ْ.

من تشابه المثلثات نحصل على:

وهذه تكافئ المعادلة التربيعية: x²-x-1=0 و هذه نفس صورة المعادلة التي حصلنا عليها سابقاً والتي حلها φ.

شكل آخر للمثلث الذهبي