|
إقليدس |
|

رسم تخيلي
لإقليدس |
|
ولد
في |
300
قبل
الميلاد |
|
توفي
في |
غير معروف |
|
مكان
الإقامة |
الإسكندرية،
مصر |
|
العرقية |
يوناني |
|
مجال
البحث |
الرياضيات |
|
اشتهر
بسبب |
الهندسة
الإقليدية
العناصر
لإقليدس |
إقليدس
(يونانية قديمة: Εὐκλείδης،
يوكليدس)
أو إقليدس الإسكندري،
ولد 300 قبل الميلاد، عالم رياضيات يوناني، غالبا ما ينسب إليه لقب "أبو
الهندسة". مشوار إقليدس العلمي كان في الإسكندرية في أيام حكم
بطليموس الأول (323–283 قبل الميلاد). اشتهر إقليدس بكتابه
العناصر
وهو الكتاب الأكثر تأثيرا في تاريخ الرياضيات، وقد استخدم هذا الكتاب
في تدريس الرياضيات (وخصوصا الهندسة) منذ بدايات نشره قديما حتى نهاية
القرن ال19 وبداية القرن ال20. بين ثنايا هذا الكتاب مبادئ ما يعرف
اليوم باسم الهندسة الإقليدية والذي تتكون من مجموعة من البديهيات.
أنشئ إقليدس بعض المصنفات أيضا في حقول عديدة؛ كالمنظور، القطع
المخروطي، الهندسة الكروية، ونظرية الأعداد وغيرها.
الاسم
إقليدس هو تعريب للفظ اليوناني
Εὐκλείδης،
والتي تعني "المجد
الحسن".
حياته
ما
يعرف عن حياة إقليدس قليل جدا جداً وهنالك مصادر محدودة تتحدث عنه. وفي
الواقع، المصادر الأساسية عن إقليدس كانت بعد قرون عديدة من حياته،
ومؤلفاها هما بروكلس وبابس الإسكندري. وكان لبروكلس نبذة قصيرة عن
إقليدس في مؤلفَه
التعقيب على
العناصر، المكتوب في القرن الخامس للميلاد، حيث ذكر أن إقليدس هو
مؤلف كتاب
العناصر،وأنه قد ذُكر على لسان أرخميدس، وذكر حدث عندما سأله
بطليموس الأول عن طريق قصير للهندسة عدا كتاب العناصر، أجابه قائلا "
لا يوجد طريق
ملَّكي إلى الهندسة. وعلى الرغم من ذلك، كان استشهاد "الطريق
الملكي" محل شك وسؤال نظرا لتشابهه مع قصة منایخموس مع الإسكندر
الأكبر. أما في المرجع الوحيد المتبقي، فقد ذكر فيه بابس بشكل موجز في
القرن الرابع عشر بأن أبولونيوس " قضى وقتا طويلا مع تلاميذ إقليدس،
وكان بذلك اكتسابه العادة العلمية الخاصة بإقليدس." ويعتقد البعض بأن
إقليدس قد درس في الأكاديمية الأفلاطونية في اليونان.
ما
زال والزمان المكان لمولد ووفاة إقليدس غير معروف، ويقدر بشكل قريب من
الأرقام المذكورة في المصادر المعاصرة. لا يوجد أي وصف كتابي أو مجسم
يصف الشكل الفيزيائي لإقليدس (حيث اعتاد اليونانيون على صنع تماثيل
لأشهر أعلامهم). أما بالنسبة للوصف الحالي، فهو عبارة عن وصف تخيلي
لإقليدس على يد فنانين معاصرين.
العناصر
على
الرغم من أن استنتاجات كتاب العناصر قد تم التوصل إليها على يد علماء
الرياضيات القدامى، فإن إنجاز إقليدس هو ضم جميع هذه الاستنتاجات في عمل مفرد في إطار متماسك منطقيا، مما يجعله سهل للاستعمال، بما في ذلك نظام صارم من البراهين الرياضياتية التي لا تزال
قاعدة أساسية للرياضيات خلال 23 قرنا، حيث كان أول من قام بالبرهان على
مبرهنة طاليس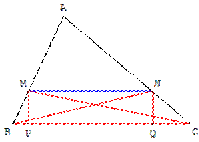 و مبرهنة فيتاغورسً و مبرهنة فيتاغورسً . .
ليس
هناك أي ذكر لإقليدس في النسخ القديمة للكتاب، وأغلب النسخ مكتوب عليها
"من إصدار ثيون" أو "محاضرات ثيون"، بينما النسخة التي تصنف كالأولى،
والموجودة في الفاتيكان، لا تذكر اسم أي مؤلف. والمرجع الوحيد الذي
يخبرنا بأن إقليدس هو مؤلف
العناصر
هو بروكلس وكتابه المرجع الذي يستند إليه المؤرخون في تحديد المؤلف،
مؤلفه
التعقيب على العناصر الذي يذكر فيه إقليدس كمؤلف للكتاب.
على
الرغم من شهرة الكتاب في مجال الهندسة الرياضية، فالكتاب أيضا يتحدث عن
نظرية الأعداد. وهو يضع بعين الاعتبار العلاقة بين الأعداد المتثالية
وأعداد ميرسين، واللاتناهي في الأعداد الأولية، وشدة إقليدس في التحليل
الرياضي
(والتي قادت إلى المبرهنة الأساسية في الحساب في تفرد التحليل للعوامل
الأولية)، وكما أن فيه خوارزمية إقليدس لإيجاد القاسم المشترك الأكبر
من رقمين.
النظام
الهندسي
الموصوف في كتاب
العناصر
عُرف قديماً باسم الهندسة، ولقد اعتبرت هي الهندسة الوحيدة الممكنة.
أما اليوم، فهي تسمى باسم الهندسة الإقليدية لفصلها عن الفرع المسمى
بالهندسة اللا إقليدية التي اكتشفها علماء الرياضيات في القرن الـ.19.

الهندسة الإقليدية
الهندسة الإقليدية
تدرس الأشكال و تخضع لمجموعة من المسلمات وضعها إقليدس في كتابه
العناصر و هي الهندسة المدرسة في المدارس و الثانويات،الهندسة
الإقليدية لا تستعمل سوى المسطرة و البركار لإنشاء الأشكال و هذا أدى
إلى ظهور مسائل هندسية لم يتم حل بعضها إلا في القرن 19 و هناك مسائل
لم يتم حلها بعد وهي:
تقسيم زاوية إلى ثلاثة أقسام
متساوية -
إنشاء
مكعب حجمه ضعف حجم مكعب معلوم
- إنشاء مربع
مساحته تساوي مساحة دائرة معينة ،
و هذه المسائل من الصعب حلها باستعمال المسطرة و البركار فقط.
العناصر الهندسية
النقطة: تمثل العناصرالأساس
للهندسة الإقليدية ، لآيمكن تقسيمها أو ، و يمكن إعتبارها تقاطع خطين.
المستقيم: خط
يمكن رسمه بالمسطرة وهو طول بدون عرض، أقصر مسافة بين نقطتين
تكون على مسار مستقيمي.
القطعة: جرء من
مستقيم محصورة بين نقطتين يسميان طرفيها.
نصف مستقيم: جزء من
مستقيم محدد بنقطة هي أصله.
الدائرة: مجموع
نقط تبعد بنفس المسافة تسمى الشعاع عن نقطة معينة تسمى المركز.

مسلمات إقليدس
-
من نقطتين يمر
مستقيم وحيد.
-
المستقيم لا
نهاية له أي يمكن تمديد المستقيم من الجهتين إلى ما لانهاية.
-
من نقطة معينة و
من مجال أو قطعة ما هناك قوس دائرة وحيد .
-
كل الزوايا
المستقيمية متساوية فيما بينها .
-
لا يمرمن نقطة
سوى مستقيم وحيد موازي لمستقيم معلوم.
إنشاءات هندسية بواسطة المسطرة و
البركار يمكن إنشاء ما يلي:
مستقيمين
متوازيين -
مستقيمين
متعامدين
-
منصف زاوية
-
واسط قطعة
-
دائرة -
قطعة طولها جداء
طول قطعتين -
قطعة طولها خارج
قسمة طول قطعتين -
قطعة طولها جذر
مربع طول قطعة معينة -
زاويتان
متساويتان.
لإقليدس بعض المبادئ التي
ذكرت على لسانه ،ومنها:
'ما
قدم بدون دليل يمكن رفضه بدون دليل'
من البديهيات:
1.
الأشياء التي تساوي شيئا واحدا تكون متساوية.
2.
إذا أضيفت متساويات إلى متساويات يكون المجموع متساويا.
3.
الأشياء التي ينطبق بعضها على بعض تكون متساوية.
4. الكل أكبر من جزئه.
خوارزمية إقليدس لتحديد القاسم المشترك الأكبر
تعريف
:
خوارمية أقليدس هي تقنية تمكننا من تحديد القاسم المشترك الأكبر
بين عددين صحيحين طبيعيين.
الطريقة
:
نعتبر
a
و
b
عددين صحيحين طبيعيين بحيث
a<b.
نقوم بقسمة
b
على
a
وليكن الباقي هو
r1
ثم نقوم بقسمة
a
على
r1
وليكن الباقي هو
r2
ثم نقوم بقسمة
r1
على
r2
ولنعتبر أن الباقي هو
r3
ثم نقسم
r2
على
r3
ونكرر العملية حتى يكون الباقي هو 0.
القاسم المشترك الأكبر ل
a
و
b
هو آخر باقي غير منعدم.
- المصادر:
-
http://debart.pagesperso-orange.fr/geoplan/euclide_classique.html
http://ar.wikipedia.org/wiki/%D8%A3%D9%82%D9%84%D9%8A%D8%AF%D8%B3
http://www.mathsways.com/2012/09/algorithme-deuclide.html
|

