|
الأولى إعدادي |
التعريف:
المستقيمان المتوازيان، هما مستقيمان، إما متطابقان أو لا يشتركان في
أية نقطة. |
|
الأولى إعدادي |
طريقة 1:
إذا كان مستقيمان متعامدان،
فكل مستقيم عمودي على أحدهما يكون موازيا للآخر. |
|
الأولى إعدادي |
طريقة 2: إذا كان
مستقيمان متوازيان فكل مستقيم موازي لأحدهما يكون موازيا للآخر. |
|
الأولى إعدادي |
طريقة 3:
صورة مستقيم بتماثل مركزي هو مستقيم يوازيه. |
|
الأولى إعدادي |
طريقة 4: إذا
حدد لنا مستقيمان
(D) و (L)
مع قاطع لهما، زاويتان متناظرتان متقايستان
فإن: (D) و (L)
متوازيان. |
|
الأولى إعدادي |
طريقة
5: إذا
حدد لنا مستقيمان
(D) و (L)
مع قاطع لهما، زاويتان متبادلتان ذاخليا متقايستان
فإن: (D) و (L)
متوازيان. |
|
الأولى إعدادي |
طريقة
6: إذا
حدد لنا مستقيمان
(D) و (L)
مع قاطع لهما، زاويتان ذاخليتان من نفس الجهة متكاملتان
فإن: (D) و (L)
متوازيان. |
|
الأولى إعدادي |
طريقة
7: إذا
كان المستقيمان
(D) و (L)
حاملي ضلعين متقابلين في متوازي الأضلاع
فإن: (D) و (L)
متوازيان. |
|
الثانية إعدادي |
طريقة
8: في مثلث
ABC
إذا كانت: I
منتصف القطعة [AB]
و: J منتصف القطعة [AC]
فإن: (IJ) و (BC)
مستقيمان متوازيان. |
|
الثانية إعدادي |
طريقة 9:
صورة مستقيم بإزاحة هو مستقيم يوازيه. |
|
الثانية إعدادي |
طريقة 10:
صورة مستقيمان متوازيان بتماثل محوري هما مستقيمان متوازيان، لأن
التماثل المحوري يحافظ على توازي المستقيمات. |
|
الثالثة إعدادي |
طريقة
11: (مبرهنة طاليس العكسية)
في مثلث
ABC
إذا كانت: I
نقطة من المستقيم
(AB)
و: J نقطة من المستقيم
(AC)
و: 
و: النقط A و B
و I و النقط A
و C و J في نفس
الترتيب.
فإن: (IJ) و (BC)
مستقيمان متوازيان. |
|
الثالثة إعدادي |
طريقة
12: إذا كانت:
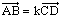
فإن: المستقيمان (AB)
و (DC) متوازيان. |
|
الثالثة إعدادي |
طريقة 13: إذا كانت :
(d) معادلته
y = mx + p
و المستقيم ('d)
معادلته y = ax + b
.
و
m = a .
فإن المستقيمان (d)
و ('d) متوازيان. |

